布隆过滤器原理与应用！

布隆过滤器它实际上是一个很长的二进制向量和一系列随机映射函数。

• 可以用于检索一个元素是否在一个集合中。

它的优点是空间效率和查询时间都远远超过一般的算法。

• 缺点是有一定的误识别率和删除困难。

布隆过滤器原理：

当一个元素被加入集合时，通过 K 个散列函数将这个元素映射成一个位数组中的 K 个点，把它们置为 1。

检索时，只要看看这些点是不是都是 1 就（大约）知道集合中有没有它了：

• 如果这些点有任何一个 0，则被检元素一定不在。
• 如果都是 1，则被检元素很可能在。

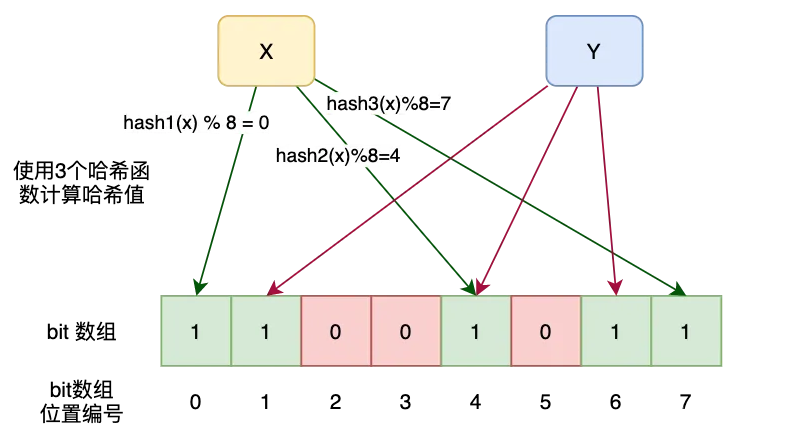
如上图，位数组的长度是８，散列函数个数是 3，先后保持两个元素ｘ，ｙ。

• 这两个元素都经过三次哈希函数生成三个哈希值，并映射到位数组的不同的位置，并置为1。

元素 x 映射到位数组的第０位，第４位，第７位，元素ｙ映射到数组的位数组的第１位，第４位，第６位。

保存元素 x 后，位数组的第4位被设置为1之后，在处理元素 y 时第4位会被覆盖，同样也会设置为 1。

• 当布隆过滤器保存的元素越多，被置为 1 的 bit 位也会越来越多。

元素 x 即便没有存储过，假设哈希函数映射到位数组的三个位都被其他值设置为 1 了。

• 对于布隆过滤器的机制来讲，元素 x 这个值也是存在的，也就是说布隆过滤器存在一定的误判率。

如何减少布隆过滤器的误判？

增加二进制位数。

增加 Hash 的次数（Hash函数个数）。

• 其实每一次 Hash 处理都是在增加数据的特征，特征越多，出现误判的概率就越小。

布隆过滤器支持删除吗?

不支持删除元素，因为多个元素可能哈希到一个布隆过滤器的同一个位置。

• 如果直接删除该位置的元素，则会影响其他元素的判断。

时间和空间效率

布隆过滤器的空间复杂度为 O(m) ，插入和查询时间复杂度都是 O(k) 。

存储空间和插入、查询时间都不会随元素增加而增大。

• 空间、时间效率都很高。

哈希函数类型

Murmur3，FNV 系列和 Jenkins 等非密码学哈希函数适合。

Murmur3 算法简单，能够平衡好速度和随机分布。

• 很多开源产品经常选用它作为哈希函数。

使用场景

缓存穿透场景:

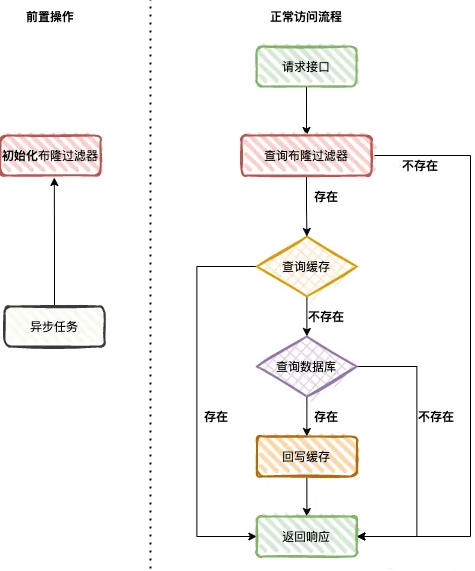
首先需要初始化布隆过滤器，然后当用户请求时，判断过滤器中是否包含该元素。

• 若不包含该元素，则直接返回不存在。

若包含则从缓存中查询数据，若缓存中也没有。

• 则查询数据库并回写到缓存里，最后给前端返回。

黑名单校验

识别垃圾邮件，只要是邮箱在黑名单中的邮件，就识别为垃圾邮件。

假设黑名单的数量是数以亿计的，存放起来就是非常耗费存储空间的。

• 布隆过滤器则是一个较好的解决方案。

把所有黑名单都放在布隆过滤器中，在收到邮件时，判断邮件地址是否在布隆过滤器中即可。

元素删除场景：

现实场景，还存在删除元素的场景，比如说商品的删除。

计数布隆过滤器：

在插入元素时给对应的 k （k 为哈希函数个数）个 Counter 的值分别加 1。

• 删除元素时给对应的 k 个 Counter 的值分别减 1。

虽然计数布隆过滤器可以解决布隆过滤器无法删除元素的问题。

• 但是：更多的资源占用，而且在很多时候会造成极大的空间浪费。

定时重新构建布隆过滤器:

从工程角度来看，定时重新构建布隆过滤器这个方案可行也可靠，同时也相对简单。

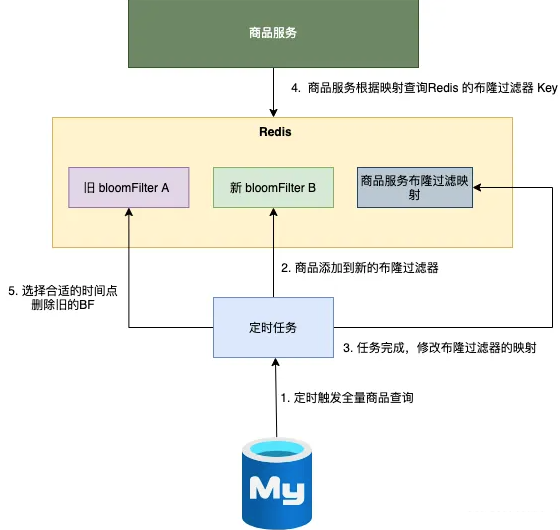
定时任务触发全量商品查询。

将商品编号添加到新的布隆过滤器。

• 任务完成，修改商品布隆过滤器的映射（从旧 A 修改成 新 B ）。

商品服务根据布隆过滤器的映射，选择新的布隆过滤器B进行相关的查询操作。

选择合适的时间点，删除旧的布隆过滤器 A。