数据结构之树！

二叉树

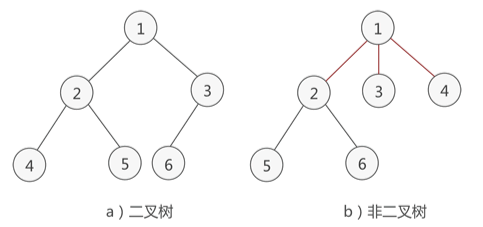
满足以下条件的树就是二叉树：

树中包含的各个节点的度不能超过 2，即只能是 0、1 或者 2。

image-20231011095850049

满二叉树

如果二叉树中除了叶子结点，每个结点的度都为2，称为满二叉树。

完全二叉树

如果二叉树中除去最后一层节点为满二叉树，且最后一层的结点依次从左到右分布，称为完全二叉树。

二叉查找树（BST）

也称二叉搜索树或二叉排序树，是指一棵空树或者具有下列性质的二叉树：

  • 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值。
  • 若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值。

AVL树

平衡二叉树又称为AVL树，是一种特殊的二查搜索树。

  • 任意节点左右子树高度之差的绝对值不超过1。

  • 平衡二叉树的搜索和插入，删除时间复杂度都是O(logn)。

平衡因子：

某节点的左子树与右子树的高度(深度)差即为该节点的平衡因子。

  • 平衡二叉树中不存在平衡因子大于 1 的节点。

在一棵平衡二叉树中，节点的平衡因子只能取 0 、1 或者 -1 ，分别对应着左右子树等高，左子树比较高，右子树比较高。

红黑树

红黑树是一种二叉查找树，但在每个节点增加一个存储位表示节点的颜色，可以是红或黑（非红即黑）。

  • 通过着色的方式的限制，红黑树确保任意节点到叶子节点的路径最长不超过最短路径的2倍。

红黑树的搜索和插入，删除时间复杂度O(logn)。

基本特点：

每个节点非红即黑。

根节点是黑的。

每个叶节点（叶节点即树尾端NULL指针或NULL节点）都是黑的。

红色节点的子节点都是黑色的。

任意节点到叶子节点的路径都包含相同数目的黑节点。

如何实现平衡：

通过改变节点颜色和左右旋转实现高度平衡。

红黑树较AVL树的优点：

AVL树是高度平衡的，频繁的插入和删除，会引起频繁的Rebalance，导致效率下降。

红黑树不是高度平衡的，算是一种折中，插入最多两次旋转，删除最多三次旋转。

  • 红黑树在查找，插入删除的性能都是O(logn)，且性能稳定。

Trie树

Trie树（前缀树）是一种用于高效检索的树形数据结构，主要用于字符串处理。

Trie树主要特点：

  • 共享相同前缀的字符串路径，从而降低了空间复杂度和查询时间。