5最长回文子串

给你一个字符串 s，找到 s 中最长的 回文子串。

class Solution {
    public String longestPalindrome(String s) {
        if (s == null || s.length() < 1) {
            return "";
        }

        //定义最长回文子串的长度
        int maxLength = 1;
        //定义最长回文子串的起始位置
        int start = 0;
        
        //遍历可能的回文子串的中心位置
        for (int i = 0; i < s.length() - 1; i++) {
            //最长回文子串的长度为奇数时，中心位置为一个字符
            int oddLength = expandAroundCenter(s, i, i);
            //最长回文子串的长度为偶数时，中心位置为两个字符
            int evenLength = expandAroundCenter(s, i, i + 1);
            int length = Math.max(oddLength, evenLength);

            //找出最大长度
            if (maxLength < length) {
                maxLength = length;
                //计算start位置
                start = i - (maxLength - 1) / 2;
                
            }
        }
        //截取字符串
        return s.substring(start, start + maxLength);
    }

    //返回最长回文子串的长度
    public int expandAroundCenter(String s, int left, int right) {
        while (left >= 0 && right < s.length()) {
            if (s.charAt(left) == s.charAt(right)) {
                //边界向外扩展
                left--;
                right++;
            } else {
                break;
            }
        }
        //最后一次向外扩展不满足条件，还原该次扩展
        left++;
        right--;
        return right - left + 1;
    }
}

9回文数

给你一个整数 x ，如果 x 是一个回文整数，返回 true ，否则，返回 false 。

回文数 是指正序（从左向右）和倒序（从右向左）读都是一样的整数。

• 例如，121 是回文，而 123 不是。

class Solution {
    public boolean isPalindrome(int x) {
        // 特殊情况：
        // 当 x < 0 时，x 不是回文数
        // 同样地，如果数字的最后一位是 0，为了使该数字为回文
        // 则其第一位数字也应该是0
        // 只有 0 满足这一属性
        if (x < 0 || (x % 10 == 0 && x != 0)) {
            return false;
        }

        int revertedNumber = 0;
        while (x > revertedNumber) {
            revertedNumber = revertedNumber * 10 + x % 10;
            x /= 10;
        }

        // 当数字长度为奇数时，我们可以通过 revertedNumber/10 去除处于中位的数
        // 例如，当输入为 12321 时，在 while 循环的末尾我们可以得到 x = 12，revertedNumber = 123，
        // 由于处于中位的数字不影响回文（它总是与自己相等），所以我们可以简单地将其去除
        return x == revertedNumber || x == revertedNumber / 10;
    }
}

14最长公共前缀

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 ""。

class Solution {
    public String longestCommonPrefix(String[] strs) {
        if(strs.length == 0) {
            return "";
        }

        String result = strs[0];
        for(int i =1;i<strs.length;i++) {
            int j=0;
            for(;j<result.length() && j < strs[i].length();j++) {
                if(result.charAt(j) != strs[i].charAt(j))
                    break;
            }
            result = result.substring(0, j);
            if(result.equals("")) {
                return result;
            }
        }
        return result;
    }
}

15三数之和

给一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k 。

同时还满足 nums[i] + nums[j] + nums[k] == 0 。

返回所有和为 0 且不重复的三元组。

class Solution {
    public static List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> result = new ArrayList();
        int len = nums.length;

        if(nums == null || len < 3) {
            return result;
        }

        Arrays.sort(nums); // 排序

        for (int i = 0; i < len ; i++) {
            if(nums[i] > 0) {
                break; // 如果当前数字大于0，则三数之和一定大于0，所以结束循环
            }

            if(i > 0 && nums[i] == nums[i-1]) {
                continue; // 去重
            }

            int L = i+1;
            int R = len-1;
            while(L < R){
                int sum = nums[i] + nums[L] + nums[R];
                if(sum == 0){
                    result.add(Arrays.asList(nums[i],nums[L],nums[R]));
                    while (L<R && nums[L] == nums[L+1]) {
                        L++; // 去重
                    }
                    while (L<R && nums[R] == nums[R-1]) {
                        R--; // 去重
                    }
                    L++;
                    R--;
                } else if (sum < 0) {
                    L++;
                } else if (sum > 0) {
                    R--;
                }
            }
        }        
        return result;
    }
}

16最接近的三数之和

给一个长度为 n 的整数数组 nums 和 一个目标值 target。

请从 nums 中选出三个整数，使它们的和与 target 最接近。

返回这三个数的和。

class Solution {
    public int threeSumClosest(int[] nums, int target) {
        Arrays.sort(nums);
        int result = nums[0] + nums[1] + nums[2];

        for(int i=0;i<nums.length;i++) {
            int start = i+1, end = nums.length - 1;
            while(start < end) {
                int sum = nums[start] + nums[end] + nums[i];
                if(Math.abs(target - sum) < Math.abs(target - result)) {
                    result = sum;
                }
                if(sum > target) {
                    end--;
                } else if(sum < target) {
                    start++;
                } else {
                    return result;
                }
            }
        }
        return result;
    }
}

18四数之和

给一个由 n 个整数组成的数组 nums ，和一个目标值 target 。

请找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]]

• 0 <= a, b, c, d < n
• a、b、c 和 d 互不相同
• nums[a] + nums[b] + nums[c] + nums[d] == target

class Solution {
    public List<List<Integer>> fourSum(int[] nums, int target) {
        Arrays.sort(nums);
        List<List<Integer>> res = new ArrayList<>();
        int length = nums.length;
        for (int i = 0; i < length - 3; i++) {
            // 跳过重复值
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }
            // 最小合都大于目标值，说明无解
            if ((long) nums[i] + nums[i + 1] + nums[i + 2] + nums[i + 3] > target) {
                break;
            }
            // 最大合小于目标值，说明i太小了，继续后移
            if ((long) nums[i] + nums[length - 3] + nums[length - 2] + nums[length - 1] < target) {
                continue;
            }
            for (int j = i + 1; j < length - 2; j++) {
                // 跳过重复的数字
                if (j > i + 1 && nums[j] == nums[j - 1]) {
                    continue;
                }
                // 最小合都大于目标值，说明无解
                if ((long) nums[i] + nums[j] + nums[j + 1] + nums[j + 2] > target) {
                    break;
                }
                // 最大合小于目标值，说明i太小了，继续后移
                if ((long) nums[i] + nums[j] + nums[length - 2] + nums[length - 1] < target) {
                    continue;
                }
                int left = j + 1, right = length - 1;
                while (left < right) {
                    int x = nums[left], y = nums[right];
                    int sum = nums[i] + nums[j] + x + y;
                    if (sum == target) {
                        res.add(Arrays.asList(nums[i], nums[j], x, y));
                        // 将两个指针都往中间推移，遇到重复的数字就跳过
                        left++;
                        while (left < right && nums[left] == nums[left - 1]) {
                            left++;
                        }
                        right--;
                        while (left < right && nums[right] == nums[right + 1]) {
                            right--;
                        }
                    } else if (sum < target) {
                        // 和小于目标值，因为是排序过的，要想结果变大，左标就要往右移动，数字更大
                        left++;
                    } else {
                        // 同理，和大于目标值，右标就要往左移动，数字更小
                        right--;
                    }
                }
            }
        }
        return res;
    }
}

20有效的括号

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

class Solution {
    public boolean isValid(String s) {
        if (s == null || s.length() == 0) {
            return true;
        }
        Stack<Character> stack = new Stack<>();
        for (char c : s.toCharArray()) {
            if (c == '(') {
                stack.push(')');
            } else if (c == '{') {
                stack.push('}');
            } else if (c == '[') {
                stack.push(']');
            } else if (stack.isEmpty() || stack.pop() != c) {
                return false;
            }
        }
        return stack.isEmpty();
    }
}

24两两交换链表中的节点

给一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。

令 cur 表示当前到达的节点，初始时 cur = pre。

• 每次需要交换 cur 后面的两个节点。

• 如果 cur 的后面没有节点或者只有一个节点，则没有更多的节点需要交换，结束交换。

• 否则，获得 cur 后面的两个节点 node1 和 node2，通过更新节点的指针关系实现两两交换节点。

交换之前的节点关系是 cur -> node1 -> node2，交换之后的节点关系要变成 cur -> node2 -> node1。

• 完成上述操作之后，节点关系即变成 cur -> node2 -> node1。

• 再令 cur = node1，对链表中的其余节点进行两两交换，直到全部节点都被两两交换。

• 两两交换链表中的节点之后，新的链表的头节点是 pre.next，返回新的链表的头节点即可。

node1.next = node2.next
cur.next = node2
node2.next = node1

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode swapPairs(ListNode head) {
        if (head == null) {
            return null;
        }

        ListNode pre = new ListNode(-1);
        pre.next = head;
        ListNode cur = pre;

        while(cur.next != null && cur.next.next != null) {
            ListNode node1 = cur.next;
            ListNode node2 = cur.next.next;
            node1.next = node2.next;
            cur.next = node2;
            node2.next = node1;
            cur = node1;
        }
        return pre.next;
    }
}

25K个一组翻转链表

给链表的头节点 head ，每 k 个节点一组进行翻转，请返回修改后的链表。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
        public ListNode reverseKGroup(ListNode head, int k) {
        if (head == null || head.next == null) {
            return head;
        }
        ListNode tail = head;
        for (int i = 0; i < k; i++) {
            //剩余数量小于k的话，则不需要反转。
            if (tail == null) {
                return head;
            }
            tail = tail.next;
        }
        // 反转前 k 个元素
        ListNode newHead = reverse(head, tail);
        //下一轮的开始的地方就是tail
        head.next = reverseKGroup(tail, k);

        return newHead;
    }

    /*
        左闭又开区间
     */
    private ListNode reverse(ListNode head, ListNode tail) {
        ListNode pre = null;
        ListNode next = null;
        while (head != tail) {
            next = head.next;
            head.next = pre;
            pre = head;
            head = next;
        }
        return pre;

    }
}

26删除排序数组中的重复项

给一个 非严格递增排列 的数组 nums 。

请你 原地 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。

元素的 相对顺序 应该保持 一致 。

然后返回 nums 中唯一元素的个数。

class Solution {
    public int removeDuplicates(int[] nums) {
        if (nums.length == 0) {
            return 0;
        }
        int i = 0;
        for (int j = 1; j<nums.length; j++) {
            if (nums[i] != nums[j]) {
                i++;
                nums[i] = nums[j];
            }
        }
        return i+1;
    }
}

27移除元素

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素。

元素的顺序可能发生改变。

然后返回 nums 中与 val 不同的元素的数量。

class Solution {
    public int removeElement(int[] nums, int val) {
        int i = 0;
        for (int j = 0; j < nums.length; j++) {
            if (nums[j] != val) {
                nums[i] = nums[j];
                i++;
            }
        }
        return i;
    }
}

33搜索旋转排序数组

整数数组 nums 按升序排列，数组中的值 互不相同 。

给 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target 。

• 则返回它的下标，否则返回 -1 。

如果用二分法去分割这个数组，则肯定是一个区间为有序，另一个区间为无序。

target可以通过对左右两边界的对比，得知这个数是否在有序区间里。

如果在，则对这个有序区间进行二分，如果不是，则target肯定是在无序区间。

在无序区间中二分也是一个道理，肯定回出现一个有序一个无序，然后继续判断即可，最终得出结果。

class Solution {
    public int search(int[] nums, int target) {
        if (nums == null || nums.length == 0) {
            return -1;
        }

        int start = 0;
        int end = nums.length - 1;
        int mid;

        while (start <= end) {
            mid = start + (end - start) / 2;
            if (nums[mid] == target) {
                return mid;
            }

            //前半部分有序,注意此处用小于等于
            if (nums[start] <= nums[mid]) {
                //target在前半部分
                if (target >= nums[start] && target < nums[mid]) {
                    end = mid - 1;
                } else {
                    start = mid + 1;
                }
            } else {
                if (target <= nums[end] && target > nums[mid]) {
                    start = mid + 1;
                } else {
                    end = mid - 1;
                }
            }

        }
        return -1;
    }
}

34在排序数组中查找元素的第一个和最后一个位置

给一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。

• 请找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

public class Solution {
    public int[] searchRange(int[] nums, int target) {
        int len = nums.length;
        if (len == 0) {
            return new int[]{-1, -1};
        }

        int firstPosition = findFirstPosition(nums, target);
        if (firstPosition == -1) {
            return new int[]{-1, -1};
        }

        int lastPosition = findLastPosition(nums, target);
        return new int[]{firstPosition, lastPosition};
    }

    private int findFirstPosition(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;
        while (left < right) {
            int mid = left + (right - left) / 2;
            // 小于一定不是解
            if (nums[mid] < target) {
                // 下一轮搜索区间是 [mid + 1..right]
                left = mid + 1;
            } else {
                // nums[mid] >= target，下一轮搜索区间是 [left..mid]
                right = mid;
            }
        }

        // 退出循环以后不能确定 nums[left] 是否等于 target，因此需要再判断一次
        if (nums[left] == target) {
            return left;
        }
        return -1;
    }

    private int findLastPosition(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;
        while (left < right) {
            int mid = left + (right - left + 1) / 2;
            if (nums[mid] > target) {
                // 下一轮搜索区间是 [left..mid - 1]
                right = mid - 1;
            } else {
                // 下一轮搜索区间是 [mid..right]
                left = mid;
            } 
        }
        // 主程序先执行 findFirstPosition，能执行到 findLastPosition 说明数组中一定存在等于 target 的元素，因此这里不用判断 nums[left] 是否等于 target
        return left;
    }
}

46全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列。

class Solution {
    private List<List<Integer>> resList = new ArrayList<>();
    private List<Integer> list = new ArrayList<>();
    private boolean[] flag;

    public List<List<Integer>> permute(int[] nums) {
        flag = new boolean[nums.length];
        backTracking(nums);
        return resList;
    }
 
    public void backTracking(int[] nums) {
        if (list.size() == nums.length) {
            resList.add(new ArrayList<>(list));
            return;
        }
 
        for (int i = 0; i < nums.length; i++) {
            if (flag[i]) {
                continue;
            }

            flag[i] = true;
            list.add(nums[i]);

            backTracking(nums);
            
            list.remove(list.size() - 1);
            flag[i] = false;
        }
    }
}

54螺旋矩阵

给一个 m 行 n 列的矩阵 matrix 。

请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        int col = 0, cols = matrix[0].length - 1, row = 0, rows = matrix.length - 1;
        List<Integer> list = new ArrayList<>();
        int total = matrix.length * matrix[0].length;
        int num = 1;
        while (num <= total) {
            for (int i = col; i <= cols && num <= total ; i++) { //从左到右
                list.add(matrix[row][i]);
                num++;
            }
            row++;
            for (int i = row; i <= rows && num <= total ; i++) { //从上到下
                list.add(matrix[i][cols]);
                num++;
            }
            cols--;
            for (int i = cols; i >= col && num <= total ; i--) { //从右到左
                list.add(matrix[rows][i]);
                num++;
            }
            rows--;
            for (int i = rows; i >= row && num <= total ; i--) { //从下到上
                list.add(matrix[i][col]);
                num++;
            }
            col++;
        }
        return list;
    }
}

57插入区间

示例 1：

输入：intervals = [[1,3],[6,9]], newInterval = [2,5]
输出：[[1,5],[6,9]]

示例 2：

输入：intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
输出：[[1,2],[3,10],[12,16]]
解释：这是因为新的区间 [4,8] 与 [3,5],[6,7],[8,10] 重叠

class Main {
    public int[][] merge(int[][] s, int[] k) {
        int[][] result = new int[s.length + 1][2];
        int index = 0,int i = 0;

        //1.没有相交的情况
        while(i < s.length && k[0] > s[i][1]) {
            result[index++] = s[i++];
        }

        //2.有相交的情况
        while(i < s.length && s[i][0] <= k[1]){
            k[0] = Math.min(k[0], s[i][0]);
            k[1] = Math.max(k[1], s[i++][1]);
        }

        //3.插入数组区间
        result[index++] = k;
        
        //4.剩下的也要放到数组中
        while(i < s.length) {
            result[index++] = s[i++];
        }

        //5.数组拷贝扩容
        return Arrays.copyOf(result, index);
    }
}

61旋转链表

给一个链表的头节点 head ，旋转链表，将链表每个节点向右移动 k 个位置。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode rotateRight(ListNode head, int k) {
        if (head == null) {
            return head;
        }

        // 计算链表中节点个数
        int len = calculateLen(head);
        k = k%len;

        // 慢指针初始指向头节点
        ListNode slow = head;
        // 快指针初始指向头节点
        ListNode fast = head;

        // 快指针先向前移动k步
        for(int i = 0; i < k; i++) {
            fast= fast.next;
        }

        // 快慢指针同时向前移动，直到快指针指向的节点的
        // 下一个节点为null
        while (fast.next != null) {
            fast = fast.next;
            slow = slow.next;
        }

        // 快指针此时在链表末尾
        // 然后其指向的节点的后继指针指向头节点
        // 这时链表首尾相连成环
        fast.next = head;
        // 新的头节点是慢指针所指节点的下一个节点
        head = slow.next;
        // 慢指针所指节点的的后继指针指向null
        // 断开环
        slow.next = null;
        return head;
    }

    private int calculateLen(ListNode head){
        int len = 0;
        while (head!=null) {
            head = head.next;
            len++;
        }
        return len;
    }
}

64最小路径和

给定一个包含非负整数的 m x n 网格 grid 。

请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

class Solution {
    public int minPathSum(int[][] grid) {
        for(int i = 0; i < grid.length; i++) {
            for(int j = 0; j < grid[0].length; j++) {
                if(i == 0 && j == 0) {
                    continue;
                } else if(i == 0) {
                    grid[i][j] = grid[i][j - 1] + grid[i][j];
                } else if(j == 0)  {
                    grid[i][j] = grid[i - 1][j] + grid[i][j];
                } else {
                    grid[i][j] = Math.min(grid[i - 1][j], grid[i][j - 1]) + grid[i][j];
                }
            }
        }
        return grid[grid.length - 1][grid[0].length - 1];
    }
}

66加一

给定一个由 整数 组成的 非空 数组所表示的非负整数，在该数的基础上加一。

最高位数字存放在数组的首位，数组中每个元素只存储单个数字。

class Solution {
    public int[] plusOne(int[] digits) {
        int n = digits.length;
        for (int i = n - 1; i >= 0; --i) {
            if (digits[i] != 9) {
                ++digits[i];
                for (int j = i + 1; j < n; ++j) {
                    digits[j] = 0;
                }
                return digits;
            }
        }

        // digits 中所有的元素均为 9
        int[] ans = new int[n + 1];
        ans[0] = 1;
        return ans;
    }
}

70爬楼梯

假设正在爬楼梯，需要 n 阶才能到达楼顶。

每次可以爬 1 或 2 个台阶。

有多少种不同的方法可以爬到楼顶呢？

class Solution {
    public int climbStairs(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        for(int i = 2; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

class Solution {
    public int climbStairs(int n) {
        int a = 1, b = 1, sum;
        for(int i = 0; i < n - 1; i++){
            sum = a + b;
            a = b;
            b = sum;
        }
        return b;
    }
}

75颜色分类

给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ，原地 对它们进行排序。

• 使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

class Solution {
    public void sortColors(int[] nums) {
        if (nums == null || nums.length == 0) {
            return;
        }
        int p0 = 0, p2 = nums.length - 1;
        for (int i = 0; i<= p2;i++) {
            //当我们将nums[i]与nums[p2]进行交换之后，新的nums[i]可能仍然是2
            while (i <= p2 && nums[i] == 2) {
                swap(nums, i, p2);
                p2--;
            }
            if (nums[i] == 0) {
                swap(nums, i, p0);
                p0++;
            }
        }
    }
    private void swap(int[] nums, int a, int b) {
        int temp = nums[a];
        nums[a] = nums[b];
        nums[b] = temp;
    }
}

78子集

给一个整数数组 nums ，数组中的元素 互不相同 。

返回该数组所有可能的子集。

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        backtrack(0, nums, res, new ArrayList<Integer>());
        return res;

    }

    private void backtrack(int i, int[] nums, List<List<Integer>> res, ArrayList<Integer> tmp) {
        res.add(new ArrayList<>(tmp));
        for (int j = i; j < nums.length; j++) {
            tmp.add(nums[j]);
            backtrack(j + 1, nums, res, tmp);
            tmp.remove(tmp.size() - 1);
        }
    }
}

82删除排序链表中的重复元素II

给定一个已排序的链表的头head，删除原始链表中所有重复数字的节点，只留下不同的数字。

返回 已排序的链表。

class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        if (head == null) {
            return head;
        }
        
        ListNode dummy = new ListNode(0, head);

        ListNode cur = dummy;
        while (cur.next != null && cur.next.next != null) {
            if (cur.next.val == cur.next.next.val) {
                int x = cur.next.val;
                while (cur.next != null && cur.next.val == x) {
                    cur.next = cur.next.next;
                }
            } else {
                cur = cur.next;
            }
        }

        return dummy.next;
    }
}

83删除排序链表中的重复元素

给定一个已排序的链表的头head，删除所有重复的元素，使每个元素只出现一次。

返回 已排序的链表。

class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        ListNode cur = head;
        while (cur != null && cur.next != null) {
            if (cur.val == cur.next.val) {
                cur.next = cur.next.next;
            } else {
                cur = cur.next;
            }
        }
        return head;
    }
}

88合并两个有序数组

给两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n。

• 分别表示 nums1 和 nums2 中的元素数目。

请 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int p1 = m - 1;
        int p2 = n - 1;
        int p = n + m - 1;
        while (p1 >= 0 && p2 >= 0) {
            nums1[p--] = (nums1[p1] < nums2[p2] ? nums2[p2--] : nums1[p1--]);
        }
        while (p2 >= 0) {
            nums1[p--] = nums2[p2--];
        }
    }
}

92反转链表II

给单链表的头指针 head 和两个整数 left 和 right ，其中 left <= right 。

请反转从位置 left 到位置 right 的链表节点，返回 反转后的链表 。

第一步：

• 找到待反转节点的前一个节点。

第二步：

• 反转 m 到 n 这部分。

第三步：

• 将反转的起点的 next 指向反转的后面一部分。

第四步：

• 将第一步找到的节点指向反转以后的头节点。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseBetween(ListNode head, int m, int n) {
        ListNode res = new ListNode(0);
        res.next = head;
        ListNode node = res;

        //找到需要反转的那一段的上一个节点。
        for (int i = 1; i < m; i++) {
            node = node.next;
        }

        //node.next就是需要反转的这段的起点
        ListNode nextHead = node.next;
        ListNode next = null;
        ListNode pre = null;

        //反转m到n这一段
        for (int i = m; i <= n; i++) {
            next = nextHead.next;
            nextHead.next = pre;
            pre = nextHead;
            nextHead = next;
        }

        //将反转的起点的next指向next
        node.next.next = next;
        //需要反转的那一段的上一个节点的next节点指向反转后链表的头结点
        node.next = pre;
        return res.next;
    }
}

94二叉树的中序遍历

递归

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        inorder(root, result);
        return result;
    }
    private void inorder(TreeNode root, List<Integer> result) {
        if (root == null) {
            return;
        }
        inorder(root.left, result);
        result.add(root.val);
        inorder(root.right, result);
    }
}

时间复杂度：O(n)，其中 n 为二叉树节点的个数，二叉树的遍历中每个节点会被访问一次且只会被访问一次。

空间复杂度：O(n)，空间复杂度取决于递归的栈深度，而栈深度在二叉树为一条链的情况下会达到 O(n) 的级别。

栈

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        while(root != null || !stack.isEmpty()) {
            while(root!=null) {
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            result.add(root.val);
            root = root.right;
        }
        return result;
    }
}

98验证二叉搜索树

给一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    long pre = Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        if (root == null) {
            return true;
        }
        // 访问左子树
        if (!isValidBST(root.left)) {
            return false;
        }
        // 访问当前节点：如果当前节点小于等于中序遍历的前一个节点，说明不满足BST，返回 false；否则继续遍历
        if (root.val <= pre) {
            return false;
        }
        pre = root.val;
        // 访问右子树
        return isValidBST(root.right);
    }
}

103二叉树的锯齿形层序遍历

给二叉树的根节点root ，返回其节点值的 锯齿形层序遍历 。

• 即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if (root == null) {
            return res;
        }

        //创建队列，保存节点
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);//先把节点加入到队列中

        boolean leftToRight = true;//第一步先从左边开始打印
        while (!queue.isEmpty()) {
            //记录每层节点的值
            List<Integer> level = new ArrayList<>();

            //统计这一层有多少个节点
            int count = queue.size();

            //遍历这一层的所有节点，把他们全部从队列中移出来，顺便
            //把他们的值加入到集合level中，接着再把他们的子节点（如果有）
            //加入到队列中
            for (int i = 0; i < count; i++) {
                //poll移除队列头部元素（队列在头部移除，尾部添加）
                TreeNode node = queue.poll();

                //判断是从左往右打印还是从右往左打印
                if (leftToRight) {
                    //如果从左边打印，直接把访问的节点值加入到列表level的末尾即可
                    level.add(node.val);
                } else {
                    //如果是从右边开始打印，每次要把访问的节点值
                    //加入到列表的最前面
                    level.add(0, node.val);
                }
                //左右子节点如果不为空会被加入到队列中
                if (node.left != null) {
                    queue.add(node.left);
                }
                if (node.right != null) {
                    queue.add(node.right);
                }
            }
            //把这一层的节点值加入到集合res中
            res.add(level);
            //改变下次访问的方向
            leftToRight = !leftToRight;
        }
        return res;
    }
}

105从前序与中序遍历序列构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历

inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

理解遍历顺序：

先序遍历（preorder）：根节点 -> 左子树 -> 右子树

中序遍历（inorder）：左子树 -> 根节点 -> 右子树

利用先序遍历的第一个元素作为根节点：

• 先序遍历的第一个元素总是当前子树的根节点。

在中序遍历中找到根节点的位置：

• 这个位置将中序遍历分为左子树和右子树。

递归构建左子树和右子树：

• 使用中序遍历中根节点左侧的数组构建左子树

  • 使用先序遍历中根节点之后的元素构建左子树

• 使用中序遍历中根节点右侧的数组构建右子树

  • 使用先序遍历中左子树之后（即根节点之后紧接着的元素）的元素构建右子树。

递归终止条件：

• 当先序遍历或中序遍历的数组为空时，返回null。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

public class Solution {  
    public TreeNode buildTree(int[] preorder, int[] inorder) {  
        if (preorder == null || inorder == null || preorder.length != inorder.length) {  
            return null;  
        }  
        return buildTreeHelper(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);  
    }  
  
    private TreeNode buildTreeHelper(int[] preorder, int preStart, int preEnd, int[] inorder, int inStart, int inEnd) {  
        if (preStart > preEnd || inStart > inEnd) {  
            return null;  
        }  
  
        // 先序遍历的第一个元素是根节点  
        int rootVal = preorder[preStart];  
        TreeNode root = new TreeNode(rootVal);  
  
        // 在中序遍历中找到根节点的位置  
        int rootIndexInorder = inStart;  
        while (inorder[rootIndexInorder] != rootVal) {  
            rootIndexInorder++;  
        }  
  
        // 构建左子树和右子树  
        int leftSubtreeSize = rootIndexInorder - inStart;  
        root.left = buildTreeHelper(preorder, preStart + 1, preStart + leftSubtreeSize, inorder, inStart, rootIndexInorder - 1);  
        root.right = buildTreeHelper(preorder, preStart + leftSubtreeSize + 1, preEnd, inorder, rootIndexInorder + 1, inEnd);  
  
        return root;  
    }  
}

108将有序数组转换为二叉搜索树

给一个整数数组 nums ，其中元素已经按 升序 排列，请将其转换为一棵 平衡二叉搜索树。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return dfs(nums, 0, nums.length - 1);
    }

    private TreeNode dfs(int[] nums, int lo, int hi) {
        if (lo > hi) {
            return null;
        } 
        // 以升序数组的中间元素作为根节点 root。
        int mid = lo + (hi - lo) / 2;
        TreeNode root = new TreeNode(nums[mid]);
        // 递归的构建 root 的左子树与右子树。
        root.left = dfs(nums, lo, mid - 1);
        root.right = dfs(nums, mid + 1, hi); 
        return root;
    }
}

112路径总和

给二叉树的根节点 root 和一个表示目标和的整数 targetSum 。

判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。

• 如果存在，返回 true ，否则，返回 false 。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
      public boolean hasPathSum(TreeNode root, int sum) {
        if(root==null) {
            return false;
        }
        if(root.left==null&&root.right==null) {
            return sum-root.val == 0;
        } 
        return hasPathSum(root.left,sum-root.val)||hasPathSum(root.right,sum-root.val);
    }
}

时间复杂度：O(N)，其中 N 是树的节点数，对每个节点访问一次。

113路径总和II

给二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

采用深度优先搜索的方式，遍历每一条从根节点到叶子节点的路径。

当我们遍历到叶子节点，且此时路径和恰为目标和时，就找到了一条满足条件的路径。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    List<List<Integer>> result = new ArrayList<List<Integer>>();
    List<Integer> list = new ArrayList<>();
    public List<List<Integer>> pathSum(TreeNode root, int sum) {
        dfs(root, sum);
        return result;
    }

    public void dfs(TreeNode root, int sum) {
        if (root == null) {
            return;
        }
        list.add(root.val);
        sum = sum - root.val;

        if (root.left == null && root.right == null && sum == 0) {
            result.add(new ArrayList<>(list));
        }

        dfs(root.left, sum);
        dfs(root.right, sum);

        list.remove(list.size() - 1);
    }
}

时间复杂度：O(N^2)，其中 N 是树的节点数。

空间复杂度：O(N)，其中 N 是树的节点数，空间复杂度主要取决于栈空间的开销，栈中的元素个数不会超过树的节点数。

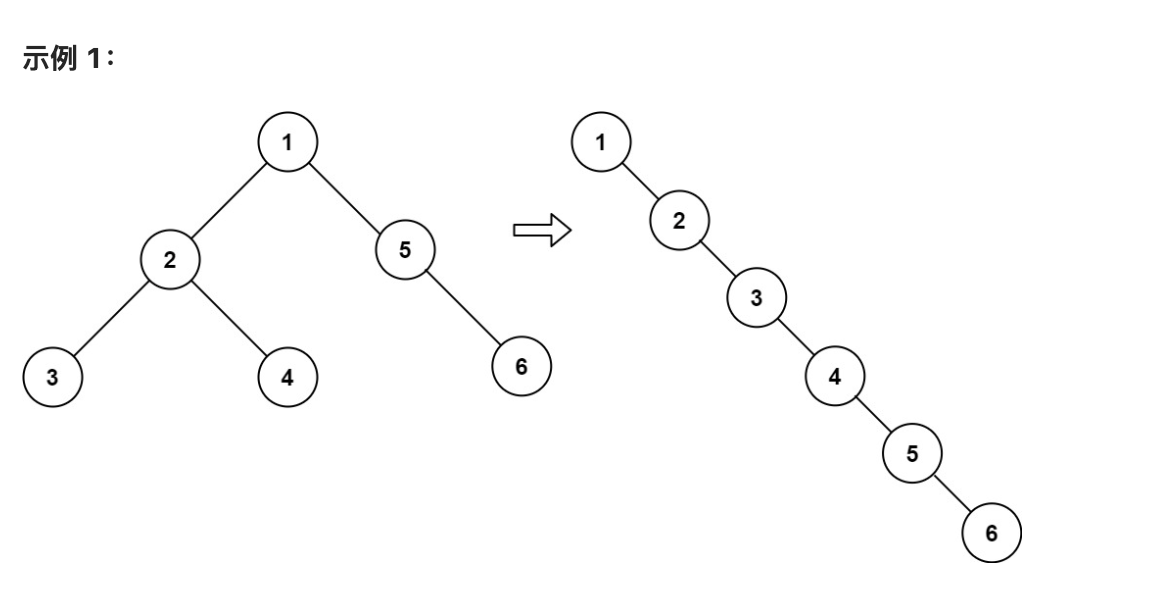
114二叉树展开为链表

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 * int val;
 * TreeNode left;
 * TreeNode right;
 * TreeNode() {}
 * TreeNode(int val) { this.val = val; }
 * TreeNode(int val, TreeNode left, TreeNode right) {
 * this.val = val;
 * this.left = left;
 * this.right = right;
 * }
 * }
 */
class Solution {
    public void flatten(TreeNode root) {
        while (root != null) {
            // 左子树为 null，直接考虑下一个节点
            if (root.left == null) {
                root = root.right;
            } else {
                // 找左子树最右边的节点
                TreeNode pre = root.left;
                while (pre.right != null) {
                    pre = pre.right;
                }
                // 将原来的右子树接到左子树的最右边节点
                pre.right = root.right;
                // 将左子树插入到右子树的地方
                root.right = root.left;
                root.left = null;
                // 考虑下一个节点
                root = root.right;
            }
        }
    }
}

121买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。

• 设计一个算法来计算所能获取的最大利润。

返回可以从这笔交易中获取的最大利润。

如果不能获取任何利润，返回 0 。

public class Solution {
    public int maxProfit(int prices[]) {
        int minPrice = Integer.MAX_VALUE;
        int maxProfit = 0;
        for (int i = 0; i < prices.length; i++) {
            if (prices[i] < minPrice) {
                minPrice = prices[i];
            } else if (prices[i] - minPrice > maxProfit) {
                maxProfit = prices[i] - minPrice;
            }
        }
        return maxProfit;
    }
}

122买卖股票的最佳时机II

给一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，可以决定是否购买和/或出售股票。

在任何时候 最多 只能持有 一股 股票。

• 也可以先购买，然后在 同一天 出售。

返回 能获得的 最大 利润 。

class Solution {
    public int maxProfit(int[] prices) {
        int profit = 0;
        for (int i = 1; i < prices.length; i++) {
            int temp = prices[i] - prices[i - 1];
            if (temp > 0) {
                profit += temp;
            }
        }
        return profit;
    }
}

125验证回文串

如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后，短语正着读和反着读都一样。

• 则可以认为该短语是一个 回文串 。

字母和数字都属于字母数字字符。

给一个字符串 s，如果它是 回文串 ，返回 true ，否则，返回 false 。

class Solution {
    public boolean isPalindrome(String s) {
        int left = 0, right = s.length() -1;
        while(left<right) {
            while(left<right&&!Character.isLetterOrDigit(s.charAt(left))) {
                left++;
            }
            while(left<right&&!Character.isLetterOrDigit(s.charAt(right))) {
                right--;
            }
            if (left<right&&Character.toLowerCase(s.charAt(left))!=Character.toLowerCase(s.charAt(right))) {
                return false;
            }
            left++;
            right--;
        }
        return true;
    }
}

129求根节点到叶节点数字之和

给一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。

每条从根节点到叶节点的路径都代表一个数字：

• 例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。

计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int sumNumbers(TreeNode root) {
        return dfs(root, 0);
    }

    public int dfs(TreeNode root, int prevSum) {
        if (root == null) {
            return 0;
        }
        int sum = prevSum * 10 + root.val;
        if (root.left == null && root.right == null) {
            return sum;
        } else {
            return dfs(root.left, sum) + dfs(root.right, sum);
        }
    }
}

时间复杂度：

• O(n)，其中 n 是二叉树的节点个数，对每个节点访问一次。

空间复杂度：

• O(n)，其中 n 是二叉树的节点个数。空间复杂度主要取决于递归调用的栈空间，递归栈的深度等于二叉树的高度，最坏情况下，二叉树的高度等于节点个数，空间复杂度为 O(n)。

136只出现一次的数字

给一个 非空 整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。

找出那个只出现了一次的元素。

class Solution {
    public int singleNumber(int[] nums) {
        int result = 0;
        for(int num : nums) {
            result = result ^ num;
        }
        return result;
    }
}

141环形链表

给一个链表的头节点 head ，判断链表中是否有环。

使用两个快慢指针遍历链表。

• slow每次走一步，fast每次走两步。
• fast走到链表尾部无环，slow与fast重叠则有环。

若链表的起始位置等于环的起始位置：

• slow走一圈回到起始位置，fast刚好走了两圈。

若环的起始位置在链表的其他位置：

• 待slow走到环的起始位置，fast在环的任意位置，可以看成是起点不同的遍历。
• 此时slow在走一圈范围内肯定会被fast超越。
• 因为每当fast每次移动一次，fast都会靠近slow一步，如果带环，两者肯定会重叠。

public class Solution {
    public boolean hasCycle(ListNode head) {
        if (head == null || head.next == null) {
            return false;
        }
        ListNode slow = head;
        ListNode fast = head.next;
        while (slow != fast) {
            if (fast == null || fast.next == null) {
                return false;
            }
            slow = slow.next;
            fast = fast.next.next;
        }
        return true;
    }
}

142环形链表II

给定一个链表的头节点 head，返回链表开始入环的第一个节点。

public class Solution {
    public ListNode detectCycle(ListNode head) {
        if (head == null || head.next == null) {
            return null;
        }
        ListNode slow = head, fast = head;
        while(true) {
            if (fast == null || fast.next == null) {
                return null;
            }
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) {
                break;
            }
        }
        fast = head;
        while(slow != fast) {
            slow = slow.next;
            fast = fast.next;
        }
        return fast;
    }
}

143重排链表

给定一个单链表 L 的头节点 head ，单链表 L 表示为：

L0 → L1 → … → Ln - 1 → Ln

请将其重新排列后变为：

L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …

不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

目标链表即为：将原链表的左半端和反转后的右半端合并后的结果。

• 找到原链表的中点

• 我们可以使用快慢指针来 O(N)找到链表的中间节点

• 将原链表的右半端反转

• 将原链表的两端合并

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public void reorderList(ListNode head) {
        if (head == null) {
            return;
        }
        //1.找到链表中间节点
        ListNode mid = middleNode(head);
        ListNode l1 = head;
        ListNode l2 = mid.next;
        mid.next = null;
        //2.反转右端链表节点
        l2 = reverseList(l2);
        //3.链表两端合并
        mergeList(l1, l2);
    }

    public ListNode middleNode(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;
        while (fast.next != null && fast.next.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }
        return slow;
    }

    public ListNode reverseList(ListNode head) {
        ListNode pre = null;
        ListNode cur = head;
        while (cur != null) {
            ListNode temp = cur.next;
            cur.next = pre;
            pre = cur;
            cur = temp;
        }
        return pre;
    }

    public void mergeList(ListNode l1, ListNode l2) {
        ListNode tempL1;
        ListNode tempL2;
        while (l1 != null && l2 != null) {
            tempL1 = l1.next;
            tempL2 = l2.next;

            l1.next = l2;
            l1 = tempL1;

            l2.next = l1;
            l2 = tempL2;
        }
    }
}

144二叉树的前序遍历

递归

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<Integer>();
        preorder(root, result);
        return result;
    }

    public void preorder(TreeNode root, List<Integer> result) {
        if (root == null) {
            return;
        }
        result.add(root.val);
        preorder(root.left, result);
        preorder(root.right, result);
    }
}

栈

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<Integer>();
        Stack<TreeNode> stack = new Stack<>();
        while (root != null || !stack.isEmpty()) {
            while(root!=null) {
                result.add(root.val);
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            root = root.right;
        }
        return result;
    }
}

145二叉树的后序遍历

递归

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<Integer>();
        postorder(root, result);
        return result;
    }

    public void postorder(TreeNode root, List<Integer> result) {
        if (root == null) {
            return;
        }
        postorder(root.left, result);
        postorder(root.right, result);
        result.add(root.val);
    }
}

栈

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        //左，右，根
        List<Integer> result = new ArrayList<Integer>();
        Stack<TreeNode> stack = new Stack<>();
        while (root!=null || !stack.isEmpty()) {
            while(root!=null) {
                result.add(root.val);
                stack.push(root);
                root = root.right;
            }
            root = stack.pop();
            root = root.left;
        }
        Collections.reverse(result);
        return result;
    }
}

146LRU缓存机制

class DLinkedNode {
    int key;
    int value;
    DLinkedNode prev;
    DLinkedNode next;
    public DLinkedNode() {}
    public DLinkedNode(int key, int value) {
        this.key = key; 
        this.value = value;
    }
}

public class LRUCache {

    private Map<Integer, DLinkedNode> cache = new HashMap<Integer, DLinkedNode>();
    private int size;
    private int capacity;
    private DLinkedNode head, tail;

    public LRUCache(int capacity) {
        this.size = 0;
        this.capacity = capacity;
        // 使用伪头部和伪尾部节点
        head = new DLinkedNode();
        tail = new DLinkedNode();
        head.next = tail;
        tail.prev = head;
    }

    public int get(int key) {
        DLinkedNode node = cache.get(key);
        if (node == null) {
            return -1;
        }
        // 如果 key 存在，先通过哈希表定位，再移到头部
        moveToHead(node);
        return node.value;
    }

    public void put(int key, int value) {
        DLinkedNode node = cache.get(key);
        if (node == null) {
            // 如果 key 不存在，创建一个新的节点
            DLinkedNode newNode = new DLinkedNode(key, value);
            // 添加进哈希表
            cache.put(key, newNode);
            // 添加至双向链表的头部
            addToHead(newNode);
            ++size;
            if (size > capacity) {
                // 如果超出容量，删除双向链表的尾部节点
                DLinkedNode tail = removeTail();
                // 删除哈希表中对应的项
                cache.remove(tail.key);
                --size;
            }
        } else {
            // 如果 key 存在，先通过哈希表定位，再修改 value，并移到头部
            node.value = value;
            moveToHead(node);
        }
    }

    private void addToHead(DLinkedNode node) {
        node.prev = head;
        node.next = head.next;
        head.next.prev = node;
        head.next = node;
    }

    private void removeNode(DLinkedNode node) {
        node.prev.next = node.next;
        node.next.prev = node.prev;
    }

    private void moveToHead(DLinkedNode node) {
        removeNode(node);
        addToHead(node);
    }

    private DLinkedNode removeTail() {
        DLinkedNode res = tail.prev;
        removeNode(res);
        return res;
    }
}

148排序链表

给链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表 。

import java.util.*;
public class Solution {
    public ListNode sortList (ListNode head) {
        if(head == null || head.next == null) {
            return head;
        }
        
        //使用快慢指针找到中点
        ListNode slow = head, fast = head.next;
        while(fast!=null && fast.next !=null){
            slow = slow.next;
            fast = fast.next.next;
        }
        
        //分割为两个链表
        ListNode newList = slow.next;
        slow.next = null;
        
        //将两个链表继续分割
        ListNode left = sortList(head);
        ListNode right = sortList(newList);

        ListNode leftHead = new ListNode(-1);
        ListNode result = leftHead;
        
        //归并排序
        while(left != null && right != null){
            if(left.val < right.val){
                leftHead.next = left;
                left = left.next;
            } else{
                leftHead.next = right;
                right = right.next;
            }
            leftHead = leftHead.next;
        }
        
        //判断左右链表是否为空
        leftHead.next = (left != null ? left : right);
        return result.next;
    }
}

时间复杂度：O(nlogn)，其中 n 是链表的长度。

155最小栈

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

class MinStack {
    private Stack<Integer> stack;
    private Stack<Integer> minStack;
    public MinStack() {
        stack = new Stack<>();
        minStack = new Stack<>();
    }
    public void push(int x) {
        stack.push(x);
        if(minStack.isEmpty() || x <= minStack.peek()) {
            minStack.push(x);
        }
    }
    public void pop() {
        if(stack.pop().equals(minStack.peek())) {
            minStack.pop();
        }
    }
    public int top() {
        return stack.peek();
    }
    public int getMin() {
        return minStack.peek();
    }
}

155将二叉搜索树转化为排序的双向链表

将一个 二叉搜索树 就地转化为一个 已排序的双向循环链表 。

对于双向循环列表，可以将左右孩子指针作为双向循环链表的前驱和后继指针。

第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

dfs(cur): 递归法中序遍历

• 终止条件： 当节点 cur 为空，代表越过叶节点，直接返回

• 递归左子树，即 dfs(cur.left)

构建链表：

• 当 pre 为空时： 代表正在访问链表头节点，记为 head

• 当 pre 不为空时： 修改双向节点引用，即 pre.right = cur ，cur.left = pre

• 保存 cur ： 更新 pre = cur ，即节点 cur 是后继节点的 pre

递归右子树，即 dfs(cur.right)

treeToDoublyList(root)：

特例处理： 若节点 root 为空，则直接返回

初始化： 空节点 pre

转化为双向链表： 调用 dfs(root)

构建循环链表： 中序遍历完成后，head 指向头节点，pre 指向尾节点，因此修改 head 和 pre 的双向节点引用即可

返回值： 返回链表的头节点 head 即可

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val,Node _left,Node _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};
*/
class Solution {
    Node head, pre;
    public Node treeToDoublyList(Node root) {
        if(root==null) return null;
        dfs(root);

        pre.right = head;
        head.left =pre;//进行头节点和尾节点的相互指向，这两句的顺序也是可以颠倒的

        return head;

    }

    public void dfs(Node cur){
        if(cur==null) return;
        dfs(cur.left);

        //pre用于记录双向链表中位于cur左侧的节点，即上一次迭代中的cur,当pre==null时，cur左侧没有节点,即此时cur为双向链表中的头节点
        if(pre==null) head = cur;
        //反之，pre!=null时，cur左侧存在节点pre，需要进行pre.right=cur的操作。
        else pre.right = cur;
       
        cur.left = pre;//pre是否为null对这句没有影响,且这句放在上面两句if else之前也是可以的。

        pre = cur;//pre指向当前的cur
        dfs(cur.right);//全部迭代完成后，pre指向双向链表中的尾节点
    }
}

160相交链表

给两个单链表的头节点 headA 和 headB 。

请找出并返回两个单链表相交的起始节点。

如果两个链表不存在相交节点，返回 null 。

双指针

创建两个指针 pA 和 pB，分别初始化为链表 A 和 B 的头结点。然后让它们向后逐结点遍历。

当 pA到达链表的尾部时，将它重定位到链表 B 的头结点，类似的，当 pB到达链表的尾部时，将它重定位到链表 A 的头结点。

若在某一时刻 pA和 pB 相遇，则 pA/pB为相交结点。

考虑以下两个链表: A={1,3,5,7,9,11} 和 B={2,4,9,11}，相交于结点 9。

• 由于 B.length (=4) < A.length (=6)，pB比 pA少经过 2个结点，会先到达尾部。

• 将 pB重定向到 A 的头结点，pA重定向到 B 的头结点后，pB要比 pA多走 2 个结点。

• 因此，它们会同时到达交点。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {

    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        if (headA == null || headB == null) {
            return null;
        }

        ListNode head1 = headA;
        ListNode head2 = headB;

        while (head1 != head2) {
            if (head1 != null) {
                head1 = head1.next;
            } else {
                head1 = headB;
            }

            if (head2 != null) {
                head2 = head2.next;
            } else {
                head2 = headA;
            }
        }
        return head1;
    }
}

时间复杂度 : O(m+n)。

空间复杂度 : O(1)。

162寻找峰值

峰值元素是指其值严格大于左右相邻值的元素。

给一个整数数组 nums，找到峰值元素并返回其索引。

数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。

二分查找

查找时，左指针 l，右指针 r，以其保持左右顺序为循环条件。

根据左右指针计算中间位置 m，并比较 m 与 m+1 的值，如果 m 较大，则左侧存在峰值，r = m。

如果 m + 1 较大，则右侧存在峰值，l = m + 1。

public class Solution {
    public int findPeakElement(int[] nums) {
        int l = 0, r = nums.length - 1;
        while (l < r) {
            int mid = (l + r) / 2;
            if (nums[mid] > nums[mid + 1]) {
                r = mid;
            } else {
                l = mid + 1;
            }
        }
        return l;
    }
}

215数组中的第K个最大元素

class Solution {
    public int findKthLargest(int[] nums, int k) {
        return quickSort(nums, 0, nums.length - 1, nums.length - k);
    }

    public int partition(int[] nums, int left, int right){
        int pivot = nums[left];

        while(left < right){
            while(left < right && nums[right] >= pivot){
                right--;
            }
            nums[left] = nums[right];

            while(left < right && nums[left] <= pivot){
                left++;
            }
            nums[right] = nums[left];
        }
        nums[left] = pivot;
        return left;
    }

    public int quickSort(int[] nums, int left, int right, int k){
        // 如果经过一轮快排分区后pivot位置刚好是k，那么可以直接退出了
        int mid = partition(nums, left, right);
        if(mid == k){
            return nums[k];
        }else if(mid > k){
            return quickSort(nums, left, mid - 1, k);
        }else{
            return quickSort(nums, mid + 1, right, k);
        }
    }
}

时间复杂度 O(N)，空间复杂度 O(1)。

222完全二叉树的节点个数

给一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int countNodes(TreeNode root) {
        if (root == null) return 0;
        int lh = 0, rh = 0;
        TreeNode left = root, right = root;
        // 求左高
        while (left != null) {
            left = left.left;
            lh++;
        }
        // 求右高
        while (right != null) {
            right = right.right;
            rh++;
        }
        // 以 root 为根节点的树是「满二叉树」
        if (lh == rh) {
          return (int) Math.pow(2, lh) - 1;
        }
        // 否则，按照正常方式遍历
        return countNodes(root.left) + countNodes(root.right) + 1;
    }
}

229求众数II

给定一个大小为 n 的整数数组，找出其中所有出现超过 ⌊ n/3 ⌋ 次的元素。

class Solution {
    public List<Integer> majorityElement(int[] nums) {
        List<Integer> res = new ArrayList<>();
        if (nums == null || nums.length == 0) {
            return res;
        }
        // 初始化两个候选人candidate，和他们的计票
        int cand1 = nums[0], count1 = 0;
        int cand2 = nums[0], count2 = 0;

        // 摩尔投票法，分为两个阶段：配对阶段和计数阶段
        // 配对阶段
        for (int num : nums) {
            // 投票
            if (cand1 == num) {
                count1++;
                continue;
            }
            if (cand2 == num) {
                count2++;
                continue;
            }

            // 第1个候选人配对
            if (count1 == 0) {
                cand1 = num;
                count1++;
                continue;
            }
            // 第2个候选人配对
            if (count2 == 0) {
                cand2 = num;
                count2++;
                continue;
            }

            count1--;
            count2--;
        }

        // 计数阶段
        // 找到了两个候选人之后，需要确定票数是否满足大于 N/3
        count1 = 0;
        count2 = 0;
        for (int num : nums) {
            if (cand1 == num) {
                count1++;
            } else if (cand2 == num) {
                count2++;
            }
        }

        if (count1 > nums.length / 3) {
            res.add(cand1);
        }
        if (count2 > nums.length / 3) {
            res.add(cand2);
        }

        return res;
    }
}

230二叉搜索树中第K小的元素

中序遍历

二叉搜索树的中序遍历是有序的，因此只需要对二叉搜索树执行中序遍历，并返回第 k 小的值即可。

class Solution {
    public int kthSmallest(TreeNode root, int k) {
        Deque<TreeNode> d = new ArrayDeque<>();
        while (root != null || !d.isEmpty()) {
            while (root != null) {
                d.addLast(root);
                root = root.left;
            }
            root = d.pollLast();
            if (--k == 0) {
                return root.val;
            }
            root = root.right;
        }
        return -1;
    }
}

时间复杂度：

• 令 h 为树高，先到达叶子位置（最小节点位置），复杂度为 O(h)，然后找到第 k 小的元素，复杂度为 O(k)。

• 整体复杂度为 O(h + k)。

空间复杂度：

• 令 h 为树高，复杂度为 O(h)。

class Solution {
    int res, k;
    void dfs(TreeNode root) {
        if (root == null) return;
        dfs(root.left);
        if (k == 0) return;
        if (--k == 0) res = root.val;
        dfs(root.right);
    }
    public int kthSmallest(TreeNode root, int k) {
        this.k = k;
        dfs(root);
        return res;
    }
}

234回文链表

整个流程可以分为以下步骤：

找到前半部分链表的尾节点。

反转后半部分链表。

判断是否回文。

恢复链表。

返回结果。

class Solution {
    public boolean isPalindrome(ListNode head) {
        if (head == null) {
            return true;
        }

        // 找到前半部分链表的尾节点并反转后半部分链表
        ListNode firstHalfEnd = endOfFirstHalf(head);
        ListNode secondHalfStart = reverseList(firstHalfEnd.next);

        // 判断是否回文
        ListNode p1 = head;
        ListNode p2 = secondHalfStart;
        boolean result = true;
        while (result && p2 != null) {
            if (p1.val != p2.val) {
                result = false;
            }
            p1 = p1.next;
            p2 = p2.next;
        }        

        // 还原链表并返回结果
        firstHalfEnd.next = reverseList(secondHalfStart);
        return result;
    }

    private ListNode reverseList(ListNode head) {
        ListNode prev = null;
        ListNode curr = head;
        while (curr != null) {
            ListNode nextTemp = curr.next;
            curr.next = prev;
            prev = curr;
            curr = nextTemp;
        }
        return prev;
    }

    private ListNode endOfFirstHalf(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        while (fast.next != null && fast.next.next != null) {
            fast = fast.next.next;
            slow = slow.next;
        }
        return slow;
    }
}

237删除链表中的节点

class Solution {
    public void deleteNode(ListNode node) {
        node.val = node.next.val;
        node.next = node.next.next;
    }
}

257二叉树的所有路径

给一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> paths = new ArrayList<String>();
        constructPaths(root, "", paths);
        return paths;
    }

    public void constructPaths(TreeNode root, String path, List<String> paths) {
        if (root == null) {
            return;
        }
        StringBuffer pathBuilder = new StringBuffer(path);
        pathBuilder.append(String.valueOf(root.val));
        if (root.left == null && root.right == null) {
            paths.add(pathBuilder.toString());
        } else {
            pathBuilder.append("->");
            constructPaths(root.left, pathBuilder.toString(), paths);
            constructPaths(root.right, pathBuilder.toString(), paths);
        }
    }
}

时间复杂度：O(N^2)，其中 N表示节点数目。

空间复杂度：O(N^2)，其中 N表示节点数目。

300最长上升子序列

给一个整数数组 nums ，找到其中最长严格递增子序列的长度。

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4

class Solution {
    public int lengthOfLIS(int[] nums) {
        if (nums == null || nums.length == 0) {
            return 0;
        }
        int[] dp = new int[nums.length];
        Arrays.fill(dp, 1);
        int result = 0;
        for (int i = 0;i<nums.length;i++) {
            for (int j = 0;j<i;j++) {
                if (nums[j] < nums[i]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            result = Math.max(result, dp[i]);
        }
        return result;
    }
}

344反转字符串

class Solution {
    public void reverseString(char[] s) {
        int left = 0, right = s.length - 1;
        while (left < right) {
            char temp = s[left];
            s[left] = s[right];
            s[right] = temp;
            left++;
            right--;
        }
    }
}

371两整数之和

class Solution {
    public int getSum(int a, int b) {
        while (b != 0) {
            int carry = (a & b) << 1;
            a = a ^ b;
            b = carry;
        }
        return a;
    }
}

378有序矩阵中第K小的元素

给一个 n x n 矩阵 matrix ，其中每行和每列元素均按升序排序，找到矩阵中第 k 小的元素。

请注意，它是 排序后 的第 k 小元素，而不是第 k 个 不同 的元素。

class Solution {
    public int kthSmallest(int[][] matrix, int k) {
        int row = matrix.length;
        int col = matrix[0].length;
        int left = matrix[0][0];
        int right = matrix[row - 1][col - 1];
        while (left < right) {
            // 每次循环都保证第K小的数在start~end之间，当start==end，第k小的数就是start
            // 防溢出,也可以写做mid = (right +left) >> 1;
            int mid = left + (right - left) / 2;
            // 找二维矩阵中<=mid的元素总个数
            int count = findLessThanMid(matrix, mid, row, col);
            if (count < k) {
                // 第k小的数在右半部分，且不包含mid
                left = mid + 1;
            } else {
                // 第k小的数在左半部分，可能包含mid
                right = mid;
            }
        }
        return right;
    }

    private int findLessThanMid(int[][] matrix, int mid, int row, int col) {
        // 以列为单位找，找到每一列最后一个<=mid的数即知道每一列有多少个数<=mid
        int i = row - 1;
        int j = 0;
        int count = 0;
        while (i >= 0 && j < col) {
            if (matrix[i][j] <= mid) {
                // 第j列有i+1个元素<=mid
                count += i + 1;
                j++;
            } else {
                // 第j列目前的数大于mid，需要继续在当前列往上找
                i--;
            }
        }
        return count;
    }
}

时间复杂度：O(nlog(r−l))，二分查找进行次数为 O(log⁡(r−l))，每次操作时间复杂度为O(n)。

空间复杂度：O(1)。

387字符串中的第一个唯一字符

给定一个字符串 s ，找到 它的第一个不重复的字符，并返回它的索引 。

如果不存在，则返回 -1 。

class Solution {
    public int firstUniqChar(String s) {
        Map<Character, Integer> map = new HashMap<>();
        for (int i = 0; i < s.length(); i++) {
            int val = map.getOrDefault(s.charAt(i), 0);
            map.put(s.charAt(i), val + 1);
        }
        for (int i = 0; i < s.length(); i++) {
            if (map.get(s.charAt(i)) == 1) return i;
        }
        return -1;
    }
}

415字符串相加

class Solution {
    public String addStrings(String num1, String num2) {
        StringBuilder res = new StringBuilder("");
        int i = num1.length() - 1, j = num2.length() - 1, carry = 0;
        while(i >= 0 || j >= 0){
            int n1 = i >= 0 ? num1.charAt(i) - '0' : 0;
            int n2 = j >= 0 ? num2.charAt(j) - '0' : 0;
            int tmp = n1 + n2 + carry;
            carry = tmp / 10;
            res.append(tmp % 10);
            i--; 
            j--;
        }
        if(carry == 1) {
          res.append(1);
        }
        return res.reverse().toString();
    }
}

437路径总和III

给定一个二叉树的根节点 root ，和一个整数 targetSum 。

求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {

    int result = 0;

    public int pathSum(TreeNode root, int targetSum) {
        if(root == null) {
            return 0;
        }
        dfs(root, targetSum);
        pathSum(root.left, targetSum);
        pathSum(root.right, targetSum);
        return result;
    }

    private void dfs(TreeNode root, long targetSum) {
        if(root == null) {
            return;
        }
        if(root.val == targetSum) {
            result++;
        }
        dfs(root.left, targetSum - root.val);
        dfs(root.right, targetSum - root.val);
    }
}

448找到所有数组中消失的数字

给一个含 n 个整数的数组 nums ，其中 nums[i] 在区间 [1, n] 内。

请找出所有在 [1, n] 范围内但没有出现在 nums 中的数字，并以数组的形式返回结果。

遍历每个元素，对索引进行标记

• 将对应索引位置的值变为负数

遍历下索引，看看哪些索引位置上的数不是负数的

• 位置上不是负数的索引，对应的元素就是不存在的

class Solution {
    public List<Integer> findDisappearedNumbers(int[] nums) {
        //用来存放结果
        List<Integer> res = new ArrayList<>(); 
        //遍历下数组的元素，对对应的索引位置的元素作标记
        int len = nums.length;
        for(int i = 0; i < len; i++){
            int num = Math.abs(nums[i]);  //由于数组的元素有可能被*-1，所以取绝对值
            int index = num - 1;
            if(nums[index] > 0){
                nums[index] *= -1;
            }
        }      
        // 寻找没有标记的索引位置
        for(int i = 0; i < len; i++){
            if(nums[i] > 0){
                int num = i + 1;  //将索引转化为对应的元素
                res.add(num);
            }     
        }
        return res;
    }
}

450删除二叉搜索树中的节点

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。

返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

• 首先找到需要删除的节点；

• 如果找到了，删除它。

二叉搜索树的性质：

• 左子树的节点的值小于根节点的值，右子树的节点大于根节点的值。

当root的值和key相等时，有四种情况：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) {
            return null;
        }
        if (root.val > key) {
            //当前节点的值大于目标值 递归去左子树寻找
            root.left = deleteNode(root.left, key);
        } else if (root.val < key) {
            //当前节点的值小于目标值 递归去右子树寻找
            root.right = deleteNode(root.right, key);
        } else {
            //情况一可以和二三合并处理
            //情况二
            if (root.left == null) {
                return root.right;
            }
            //情况三
            if (root.right == null) {
                return root.left;
            }
            //情况四 
            //找到右节点的左子树中为空的位置
            TreeNode rightNode = root.right;
            while (rightNode.left != null) {
                rightNode = rightNode.left;
            }
            rightNode.left = root.left;
            root = root.right;
        }
        return root;
    }
}

560和为K的子数组

给一个整数数组 nums 和一个整数 k 。

请统计并返回 该数组中和为 k 的子数组的个数。

前缀和

哈希表中存放的是前缀和对应的个数，答案res中记录着每个前缀和sum[i] -k的个数

public class Solution {
    public int subarraySum(int[] nums, int k) {
        int count = 0, pre = 0;
        HashMap<Integer, Integer> mp = new HashMap<>();
        mp.put(0, 1);
        for (int i = 0; i < nums.length; i++) {
            pre += nums[i];
            if (mp.containsKey(pre - k)) {
                count += mp.get(pre - k);
            }
            mp.put(pre, mp.getOrDefault(pre, 0) + 1);
        }
        return count;
    }
}

572另一棵树的子树

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSubtree(TreeNode s, TreeNode t) {
        return dfs(s, t);
    }

    public boolean dfs(TreeNode s, TreeNode t) {
        if (s == null) {
            return false;
        }
        return check(s, t) || dfs(s.left, t) || dfs(s.right, t);
    }

    public boolean check(TreeNode s, TreeNode t) {
        if (s == null && t == null) {
            return true;
        }
        if (s == null || t == null || s.val != t.val) {
            return false;
        }
        return check(s.left, t.left) && check(s.right, t.right);
    }
}

662二叉树最大宽度

给一棵二叉树的根节点 root ，返回树的 最大宽度 。

树的 最大宽度 是所有层中最大的 宽度 。

每一层的 宽度 被定义为该层最左和最右的非空节点（即，两个端点）之间的长度。

此题求二叉树所有层的最大宽度，比较直观的方法是求出每一层的宽度，然后求出最大值。

求每一层的宽度时，因为两端点间的 null 节点也需要计入宽度，因此可以对节点进行编号。

一个编号为 index 的左子节点的编号记为 2×index，右子节点的编号记为 2×index+1，计算每层宽度时，用每层节点的最大编号减去最小编号再加 1 即为宽度。

遍历节点时，可以用广度优先搜索来遍历每一层的节点，并求出最大值。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int widthOfBinaryTree(TreeNode root) {
        if(root == null) {
            return 0;
        }

        Deque<TreeNode> queue = new LinkedList<>();
        // 根节点编号为 0
        root.val = 0;
        queue.add(root);

        int sum;
        int ans = 0;
        while(!queue.isEmpty()) {
            sum = queue.size();
            // 队头和队尾的编号值求差用来更新宽度
            ans = Math.max(ans, queue.getLast().val - queue.getFirst().val + 1);
            // 一次处理一层，进入这个循环前队列中是一层的所有非空节点
            while(sum > 0) {
                TreeNode temp = queue.remove();

                // 子节点入队前修改 val, val = 满二叉树中节点编号
                if(temp.left != null) {
                    queue.add(temp.left);
                    temp.left.val = temp.val * 2 + 1;
                }
                if(temp.right != null) {
                    queue.add(temp.right);
                    temp.right.val = temp.val * 2 + 2;
                }
                sum--;
            }
        }
        return ans;
    }
}

674最长连续递增序列

给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度。

class Solution {
    public int findLengthOfLCIS(int[] nums) {
        if (nums == null || nums.length == 0) {
            return 0;
        }
        int count = 1, result = 1;
        for (int i =0;i<nums.length - 1;i++){
            if (nums[i] < nums[i+1]){
                count++;
            }else {
                count = 1;
            }
            result = Math.max(result , count);
        }
        return result;
    }
}

704二分查找

class Solution {
    public int search(int[] nums, int target) {
        if (nums==null || nums.length == 0) {
            return -1;
        }
        int left = 0, right = nums.length - 1;
        while(left<=right){
            int middle = left + (right - left) / 2;
            if (nums[middle]==target) {
                return middle;
            } else if (nums[middle] > target) {
                right = middle - 1;
            } else {
                left = middle + 1;
            }
        }
        return -1;
    }
}

718最长重复子数组

给两个整数数组 nums1 和 nums2 ，返回 两个数组中 公共的 长度最长的子数组的长度。

输入：nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出：3
解释：长度最长的公共子数组是 [3,2,1]

动态规划

首先定义dp[i][j]表示为A[i:]和B[j:]的最长公共前缀。

dp[i][j]可以从dp[i+1][j+1]转移而来。

class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        int n = nums1.length;
        int m = nums2.length;
        int[][] dp = new int[n+1][m+1];//dp[i][j]表示从i开始的A的子串和从j开始的B的子串的最长公共前缀
        int maxs = 0;
        for(int i=1; i<=n; i++){
            for(int j=1; j<=m; j++){
                if(nums1[i-1] == nums2[j-1]){
                    dp[i][j] = dp[i-1][j-1] + 1;
                }else{
                    dp[i][j] = 0;
                }
                maxs = Math.max(maxs, dp[i][j]);
            }
        }
        return maxs;
    }
}

876链表的中间结点

快慢指针法

用两个指针 slow 与 fast 一起遍历链表。

slow 一次走一步，fast 一次走两步。

那么当 fast 到达链表的末尾时，slow 必然位于中间。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode middleNode(ListNode head) {
        ListNode slow = head, fast = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }
        return slow;
    }
}

958二叉树的完全性检验

给一棵二叉树的根节点 root ，请判断这棵树是否是一棵 完全二叉树 。

class Solution {
    public boolean isCompleteTree(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        TreeNode prev = root;
        queue.add(root);
        while (!queue.isEmpty()) {
            TreeNode node = queue.remove();
            if (prev == null && node != null) {
                return false;
            }
            if (node != null) {
                queue.add(node.left);
                queue.add(node.right);
            }
            prev = node;
        }
        return true;
    }
}

1214查找两颗二分搜索树之和

给出两棵二叉搜索树，请你从两棵树中各找出一个节点，使得这两个节点的值之和等于目标值 Target。

如果可以找到返回 True，否则返回 False。

示例 1：

输入：root1 = [2,1,4], root2 = [1,0,3], target = 5 输出：true 解释：2 加 3 和为 5。

二分法解决:

先固定一棵树的一个节点，将目标值Target减去这个节点的值，得到新的目标值target。

将这个新的目标值和另外一棵树进行比较，利用二分搜索数的特性进行查找命中，从根节点开始，如果新的目标值target和根节点的值相等，则直接返回true。

如果新的目标值比根节点小，进行左递归查找，如果新的目标值比根节点大，进行右递归。

依次类推，直到树底下的节点为空，才返回false。

固定一棵树的一个节点，查找另一棵树的节点的时间复杂度是O(logn)。

因为一棵树需要遍历，时间复杂度是O(nlogn)。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean twoSumBSTs(TreeNode root1, TreeNode root2, int target) {
        if (!root1) return false;
        if (find(root2, target - root1.val)) return true;
        return twoSumBSTs(root1.left, root2, target) || 
        twoSumBSTs(root1.right, root2, target);            
    }

    private boolean find(TreeNode node, int target) {
        if (!node) return false;
        if (node.val == target) return true;
        else if (target < node.val) return find(node.left, target);
        else return find(node.right, target);
    }
}

1539第K个缺失的正整数

设：arr = [2,3,4,5,7,11], k = 5

可以利用数组下标来得到该位置之前缺失的元素数量，例如：

i = 0，此时数组元素arr[i] = 2，在0位置上，不缺失的情况下，对应的元素应该是1，所以缺失个数为arr[i] - i - 1 = 1,因为数组下标是从0开始的，而元素是从1开始的，所以计算个数的时候，除了减掉下标值之外，还需要再减1。

按照这个方式，能计算出该数组的每个元素对应的缺失元素个数：

在这个序列中，能够通过二分查找，找到k所对应的位置，有了这个位置，就能通过对应的元素找到缺失的第k个整数。

举例来说，如果要找到k = 5，第5个缺失的元素，那么需要从一个确定的数向后或向前推算：

对于2,3,4来说，它们之前缺少1个元素，所以不考虑这些元素。

对于7来说，它之前缺少3个元素，那么从它开始往后推2个元素，就有可能是缺失的第5个元素。

前提是它后面的元素缺失数量要大于k = 5。

对于11来说，它之前缺少6个元素，要找的第5个元素，一定是在它之前缺失的，那从它开始往前推2个元素（第6个，第5个），就是要找的缺失的第5个元素。

根据这种分析，就可以在这个缺失数量的序列上进行二分查找，确定一个区间[i,j]，满足lack[i] < k <= lack[j]，则第k个缺失的数为k - (arr[i] - i - 1) + arr[i]，arr[i] - i - 1表示arr[i]位置缺少的元素个数，k - 缺失个数表示从arr[i]开始还缺少几个元素，再加上arr[i]，就是第k个缺失的元素。

class Solution {
    public int findKthPositive(int[] arr, int k) {
        // 第一个数比缺失的数要大的话，直接返回k
        if(arr[0] > k){
            return k;
        }
        // 找到缺失数量大于k的最小的位置
        int left = 0, right = arr.length;
        while(left < right){
            int mid = left + (right - left) / 2;
            int x = mid < arr.length ? arr[mid] : Integer.MAX_VALUE;
            if(x - mid - 1 >= k){
                right = mid;
            }else{
                left = mid + 1;
            }
        }
        // 第k个缺失的数 - （最小位置之前的那个数所缺失的个数） + 最小位置前面的那个数
        // 5 - （7 - 3 - 1） + 7 = 第五个缺失的数 - 7前面有3个缺失的数 + 7
        return k - (arr[left - 1] - (left - 1) - 1) + arr[left - 1];
    }
}

public int findKthPositive(int[] arr, int k) {
    int n = arr.length; // 数组长度
    int low = 0, high = n; // 初始化二分查找的上下边界

    while (low < high) {
        int mid = low + (high - low) / 2; // 计算中间位置

        // 计算当前中间位置缺失的正整数数量
        if (arr[mid] - mid - 1 >= k) {
            high = mid; // 如果缺失数量大于或等于 k，则目标在左半部分
        } else {
            low = mid + 1; // 否则，目标在右半部分
        }
    }

    // 计算当前 low 之前缺失的正整数数量
    int prev = low > 0 ? arr[low - 1] : 0;
    int prevMissingCount = prev - low;

    return prev + k - prevMissingCount; // 计算并返回第 k 个缺失的正整数
}

1143最长公共子序列

定义一个二维数组 dp 用来存储最长公共子序列的长度，其中 dp[i][j] 表示 S1 的前 i 个字符与 S2 的前 j 个字符最长公共子序列的长度。

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int n1 = text1.length(), n2 = text2.length();
        int[][] dp = new int[n1+1][n2+1];
        for (int i = 1;i <= n1;i++) {
            for (int j = 1;j<=n2;j++) {
                if(text1.charAt(i-1) == text2.charAt(j-1)) {
                    dp[i][j] = dp[i-1][j-1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
                }
            }
        }
        return dp[n1][n2];
    }
}

1614括号的最大嵌套深度

class Solution {
    public int maxDepth(String s) {
        int ans = 0, size = 0;
        for (int i = 0; i < s.length(); ++i) {
            char ch = s.charAt(i);
            if (ch == '(') {
                ++size;
                ans = Math.max(ans, size);
            } else if (ch == ')') {
                --size;
            }
        }
        return ans;
    }
}